splay tree 即伸展树
这是一种二叉排序树，重点操作在把目标节点转换为根节点，且仍保持着左边节点小，右边节点大的特性。
那么，如何实现把目标节点转换为根节点呢？我们来分类讨论一下：
假设需要把x转换为根节点
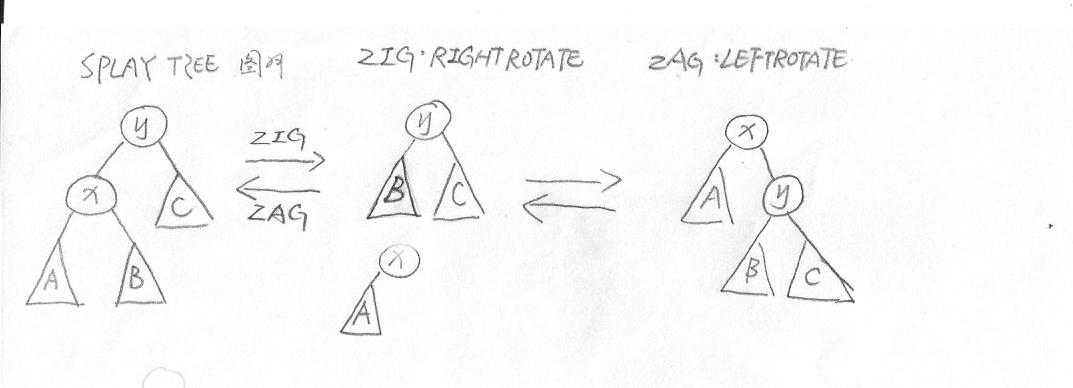
1.x为y的左孩子,且y没有父亲
操作zig（即right rotate，右旋）
1 2 3 4 5 6 7 8 9 10 11 12 | proc zig(x) y=x.father y.rightchild=x.leftchild if x.leftchild!=null x.leftchild.father=y x.father=y.father if y.father!=null if y=y.father.leftchild y.father.leftchild=x else y.father.rightchild=x y.father=x x.leftchild=y |
2.x为y的右孩子，且y没有父亲
操作zag（即left rotate，左旋）
1 2 3 4 5 6 7 8 9 10 11 12 | proc zag(x) y=x.father y.leftchild=x.rightchild if x.rightchild!=null x.rightchild.father=y x.father=y.father if y.father!=null if y=y.father.leftchild y.father.leftchild=x else y.father.rightchild=x y.father=x x.rightchild=y |
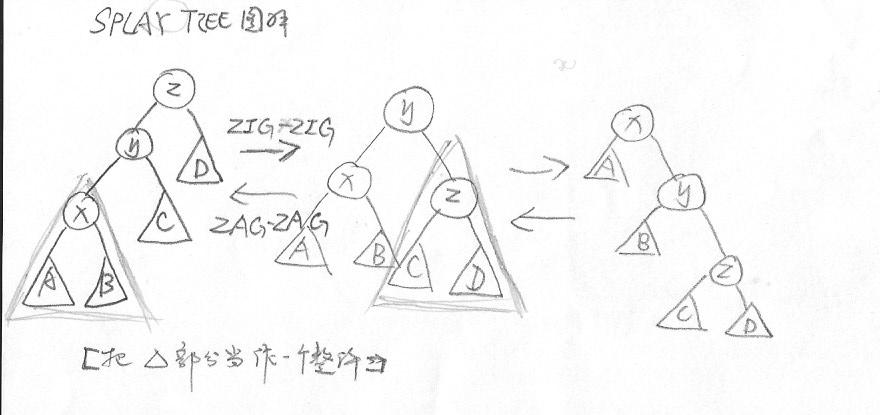
3.x为y的左孩子且y为z的左孩子:zigzig
rightrotate(y);
rightrotate(x);
rightrotate(x);
4.x为y的右孩子且y为z的右孩子:zagzag
leftrotate(y);
leftrotate(x);
leftrotate(x);
5.x为y的左孩子且y为z的右孩子：zigzag
rightrotate(x);
leftrotate(x);
leftrotate(x);
6.x为y的右孩子且y为x的左孩子：zagzig
leftrotate(x);
rightrotate(x);
rightrotate(x);
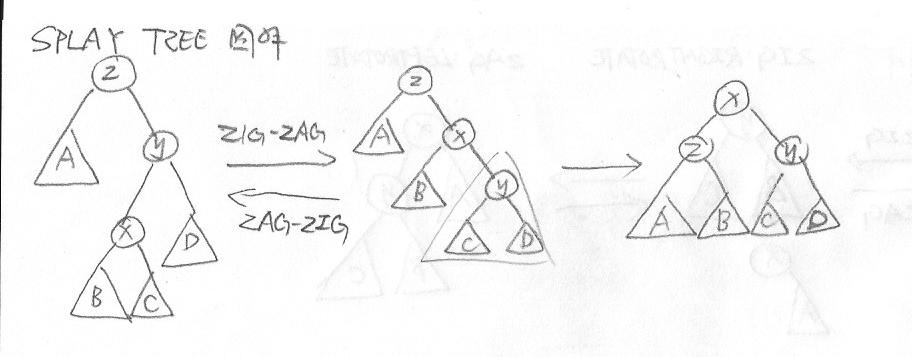注：图中的zagzig是手误。
综上所述，我们可以定义另一个过程：splay(x)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | proc splay(x) while x.father<>null p=x.father if p.father=null if x=p.leftchild rightrotate(x) else leftrotate(x) break if x=p.leftchild if p=p.father.leftchild //zig-zig rightrotate(p) rightrotate(x) else //zig-zag rightrotate(x) leftrotate(x) else if p=p.father.rightchild //zag-zag leftrotate(p) leftrotate(x) else leftrotate(x) //zag-zig rightrotate(x) root=x |
这里是昨天写的模板题
我昨天说，zig和zag可以减小代码长度。在这种政策下，效率越高越好。怎么办呢？
我们发现，zig和zag很多地方是重复的，zig把leftchild和rightchild稍微改一下就是zag，这里就拼技巧了！
对于每个节点x，左子树为x[0]，右子树为x[1]。
而对于rotate操作，改为rotate(x,kind)
这里的kind代表0左旋或1右旋。
所有的左子树就表示为x[kind]，右子树就表示为x[!kind]或x[kind^1]，这里的^是xor
代码如下：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | rotate(x,kind) y=x.father y.(kind xor 1)=x.kind if x.kind!=null x.kind.father=y x.father=y.father if y.father!=null if y=y.father.0 y.father.0=x else y.father.1=x y.father=x x.kind=y//这里的语法什么的就不要纠结了。大体思想给出来了。 |
其实很多情况，kind^1都能起到很大的作用。比如你按0,1;2,3;4,5;6,7...一对对保存数组
已知一个数a[kind]，找它的另一半（好有喜感）就可以表示为a[kind xor 1]。为什么呢？
2^1=3;3^1=2；4^1=5;5^1=4
证明以后再给（自己想去！）
一个数表示为二进制abcdef,那么它的另一半肯定就是abcde(f^1)，所以可以实现
好吧扯远了。今天就总结到这，我们下次再见。
欢迎批评指正错误，或提出问题
2015年3月28日 12:56